Code & Func

第18天。

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Return a list of all possible full binary trees with N nodes. Each element of the answer is the root node of one possible tree.

Each node of each tree in the answer must have node.val = 0.

You may return the final list of trees in any order.

Example 1:

1
Input: 7
2
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
3
Explanation: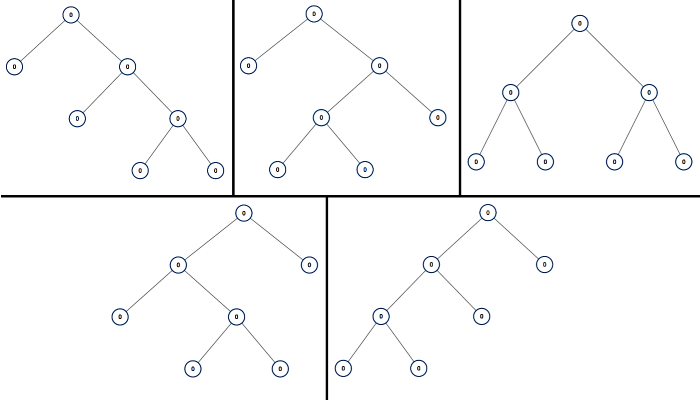

Note:

1 <= N <= 20

这道题就是一个穷举的问题，我们知道完全二叉树的节点个数一定是奇数，所以可以先把N为偶数的输入先处理掉，然后就是怎么穷举的问题了。显然，一个完全二叉树的子树一定也是完全二叉树，所以我们可以以1,3,5...,N-2的方式穷举出出左子树中节点的个数i，已知左子树节点个数，那么右子树节点的个数就为N-i-1,我们先把左子树和右子树的可能都算出来，然后就再计算它们两两组合的所有可能即可得到所有节点个数为N的完全二叉树的情况。总的来说，就是一个大问题化简成小问题的思路。所以我们可以写出如下代码：

1
TreeNode *copyTree(TreeNode *root) {
2
    if (root == nullptr) return nullptr;
3
    TreeNode *res = new TreeNode(0);
4
    res->left = copyTree(root->left);
5
    res->right = copyTree(root->right);
6
    return res;
7
}
8

9
vector<TreeNode*> allPossibleFBT(int N) {
10
    vector<TreeNode*> res;
11
    if (N % 2 == 0) return res;
12

13
    vector<vector<TreeNode*>> dp(N+1);
14
    dp[1].push_back(new TreeNode(0));
15

17 collapsed lines
16
    for(int i = 1;i < dp.size();i+=2) {
17
        // dp[i];
18
        for(int j = 1;j < i;j+=2) {
19
            vector<TreeNode*> &left = dp[j];
20
            vector<TreeNode*> &right = dp[(i-j-1)];
21
            for(auto &l: left) {
22
                for(auto &r: right) {
23
                    TreeNode *node = new TreeNode(0);
24
                    node->left = copyTree(l);
25
                    node->right = copyTree(r);
26
                    dp[i].push_back(node);
27
                }
28
            }
29
        }
30
    }
31
    return dp[N];
32
}

然后你会发现好像可以用一个数组来存在已经求解出来的结果，如果再一次求，我们可以直接返回了：

1
vector<TreeNode*> &allPossibleFBT(int N, vector<vector<TreeNode*>> &cache) {
2
    if (cache[N].size() != 0) return cache[N];
3

4
    for(int i = 1;i < N;i++) {
5
        vector<TreeNode*> &left = allPossibleFBT(i, cache);
6
        vector<TreeNode*> &right = allPossibleFBT(N - i - 1, cache);
7
        for(auto l: left) {
8
            for(auto r: right) {
9
                TreeNode *node = new TreeNode(0);
10
                node->left = l;
11
                node->right = r;
12
                cache[N].push_back(node);
13
            }
14
        }
15
    }
11 collapsed lines
16
    return cache[N];
17
}
18

19
vector<TreeNode*> allPossibleFBT(int N) {
20
    vector<TreeNode*> res;
21
    if (N % 2 == 0) return {};
22
    vector<vector<TreeNode*>> cache(21);
23

24
    cache[1].push_back(new TreeNode(0));
25
    return allPossibleFBT(N, cache);
26
}

如果熟悉动态规划的话，就会发现可以自顶向下的求解方式转成自底向上的求解方式，这里我们就不需要用递归去求解：

1
vector<TreeNode*> allPossibleFBT(int N) {
2
    vector<TreeNode*> res;
3
    if (N % 2 == 0) return res;
4

5
    vector<vector<TreeNode*>> dp(N+1);
6
    dp[1].push_back(new TreeNode(0));
7

8
    for(int i = 1;i < dp.size();i+=2) {
9
        // dp[i];
10
        for(int j = 1;j < i;j+=2) {
11
            for(auto l: dp[j]) {
12
                for(auto r: dp[i-j-1]) {
13
                    TreeNode *node = new TreeNode(0);
14
                    node->left = copyTree(l);
15
                    node->right = copyTree(r);
7 collapsed lines
16
                    dp[i].push_back(node);
17
                }
18
            }
19
        }
20
    }
21
    return dp[N];
22
}

最后，这份代码在LeetCode大概只能超过50%，如果要进一步，只有把copyTree去掉，直接赋值。这种方式是可行的，但是感觉只是在刷题时的一种技巧而已：

1
vector<TreeNode*> allPossibleFBT(int N) {
2
    vector<TreeNode*> res;
3
    if (N % 2 == 0) return res;
4

5
    vector<vector<TreeNode*>> dp(N+1);
6
    dp[1].push_back(new TreeNode(0));
7

8
    for(int i = 1;i < dp.size();i+=2) {
9
        // dp[i];
10
        for(int j = 1;j < i;j+=2) {
11
            for(auto l: dp[j]) {
12
                for(auto r: dp[i-j-1]) {
13
                    TreeNode *node = new TreeNode(0);
14
                    node->left = l;//copyTree(l);
15
                    node->right = r;//copyTree(r);
7 collapsed lines
16
                    dp[i].push_back(node);
17
                }
18
            }
19
        }
20
    }
21
    return dp[N];
22
}